BLDC的FOC矢量控制算法解析，带GIF

无意中看到一篇带动图的算法解析，很受用，分享给大家。

源地址：http://wemedia.ifeng.com/93001361/wemedia.shtml

正文开始：

--------------------------------------------------------------------------------------

常见的BLDC直流无刷电机由于采用非正弦分布的定子绕组，它的反电动势为梯形，产生的电流也是梯形的，因此会出现转矩脉动，这种转矩脉动会导致低转速时的震荡，从而产生音频噪音。具有正弦反电动势的BLDC电机称作PMSM，即永磁同步电机。它采用正弦电流驱动，减小了转矩脉动，特别适合于低转矩以及低噪声的场合。理论上BLDC的定子反电动势为梯形，但是由于制造工艺的问题，BLDC的定子反电动势通常并不是那么呈平整的梯形分布，而更趋向于正弦分布；因此BLDC也可以使用PMSM的正弦矢量控制方式。

在一些高端应用中，如机床设备或低噪声风机以及我们常见的平衡车、新能源汽车、医疗机器人、无人驾驶系统等等，平稳的转矩输出是至关重要的；它需要对负载做出快速的响应，电机的瞬时效率高，转矩平稳，且能实现位置控制，这些都离不开FOC矢量控制。

我们都知道电机的转矩正比于两个磁场向量所围成平行四边形的面积，即定子磁场与转子磁场的叉乘。当定子磁场与转子磁场夹角为90°时，所产生的力矩最大。因此电机的控制可以归结为两个磁场力的控制，因为磁场=电流x电感，那么控制就成了电流的控制。

如何保持定子磁场始终与转子磁场相差90°，这就是FOC矢量控制解决的问题。
当BLDC的三相分别通以相差120°的正弦电压时，它会在空间形成一个旋转的磁场:

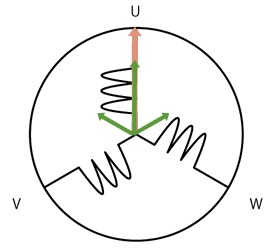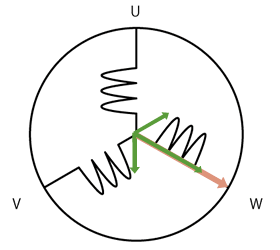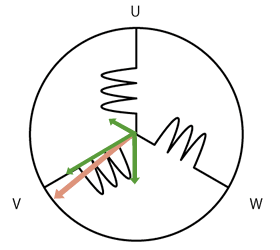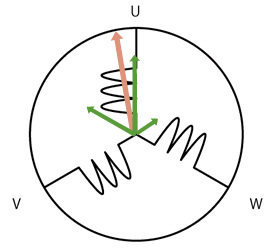
根据矢量合成原理，定子三相内的复杂定子电流矢量可以定义为：

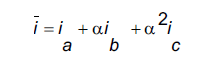
其中:

 

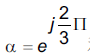
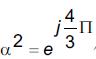
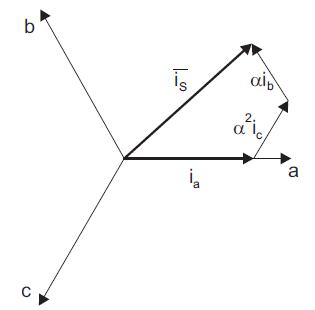
这是三相a、b、c坐标轴系统下的电流矢量。为了更好的控制它，我们将这个复杂电流矢量变换为两坐标时变系统，这就是Clarke变换：

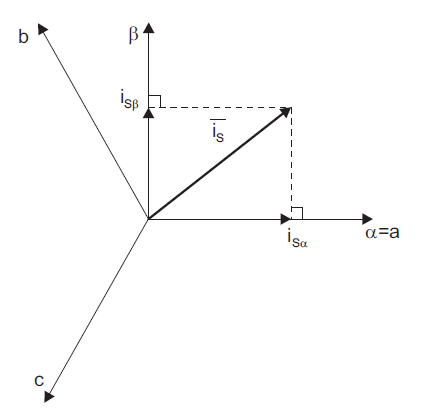
接下来，将两坐标轴时变系统变换为两坐标轴旋转系统，即Park变换：

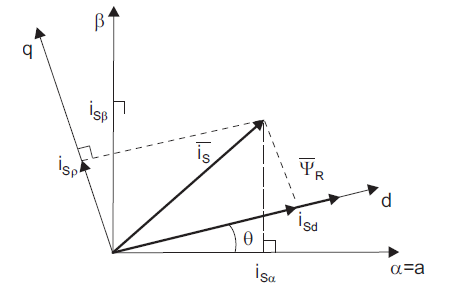
由此可得出：

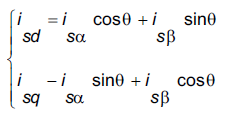
d 轴与转子磁通对齐，q轴正交与d轴，角度θ为转子磁通位置。

通过此变换，d、q轴的分量变成一个常量，现在三个相位上的电流转换为直流非时变分量，使转矩控制变得简单。

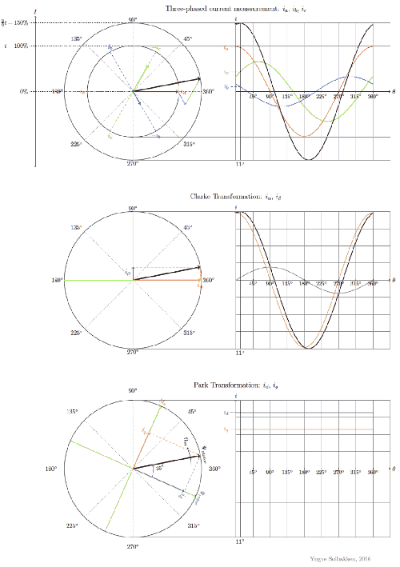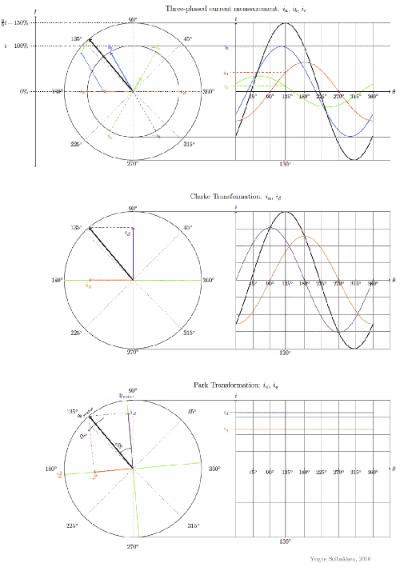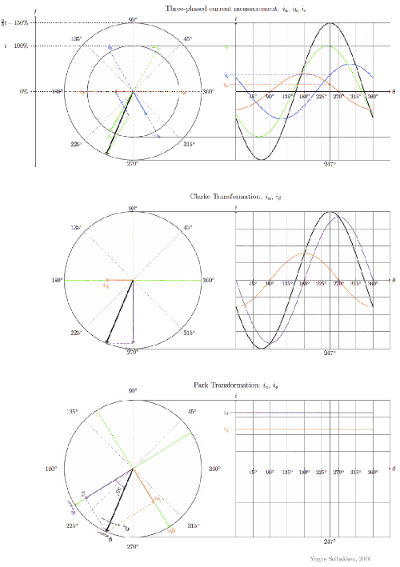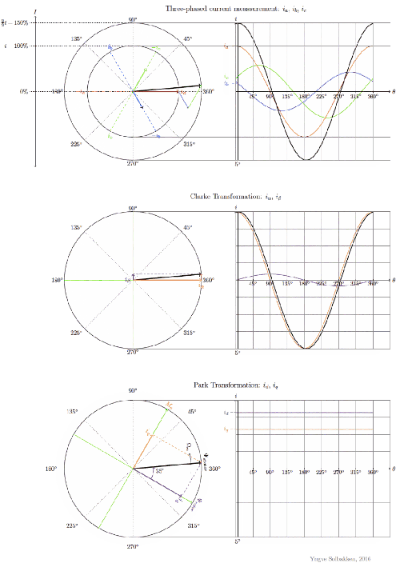
基本控制原理：

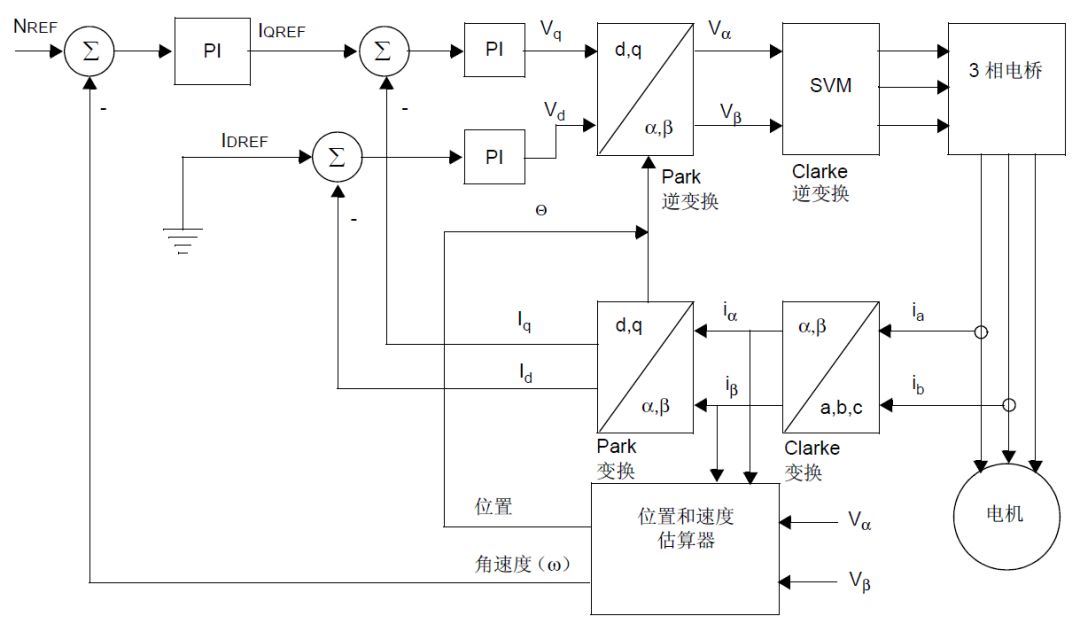
目前普遍使用SVM空间矢量调制实现正弦波发生。

再来看一下三相驱动电路：

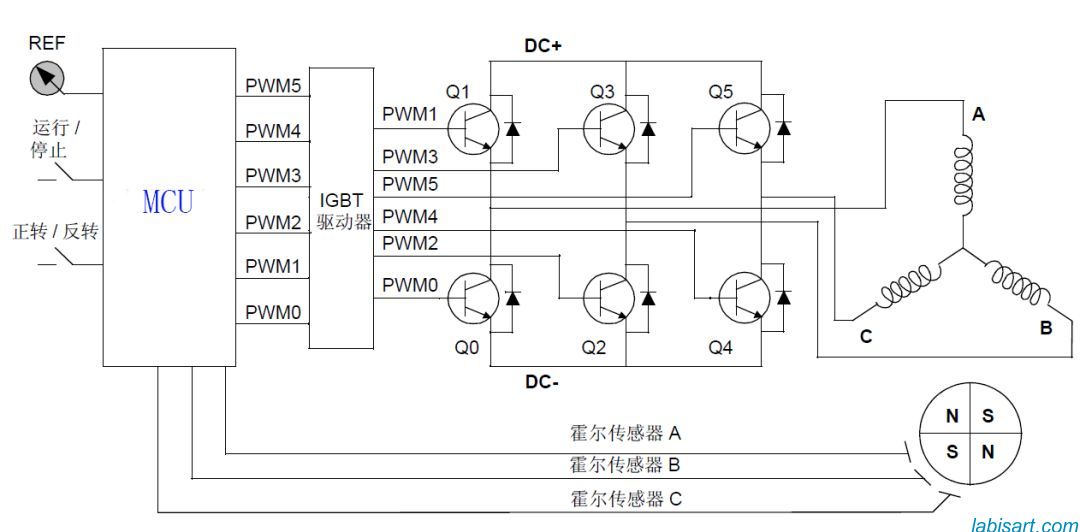
每一相连接的两个MOS管只能同时导通一个，上管导通或下管导通，我们将上管导通记为1，下管导通记为0，那么三相共有8种导通组合:

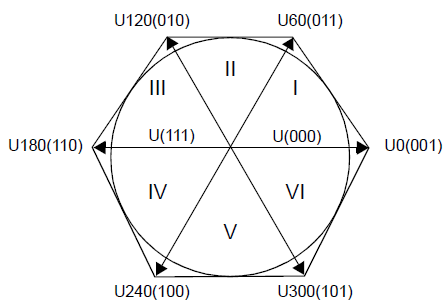
其中U(111)和U(000)为两个零矢量，因为都为1时，三相全连接到正的电源母线，任意两相之间不存在线电压，都为0时效果一样；其余的六个非零矢量在空间互差60°，空间中的其他矢量都可以由这六个基本矢量合成而来。

假设Uout位于空间U0和U60之间，那么：

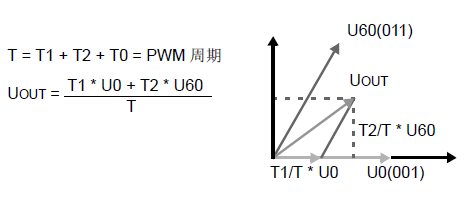
在一个PWM周期T中，U0的输出时间为T1,U60的输出时间为T2，T0为零矢量。

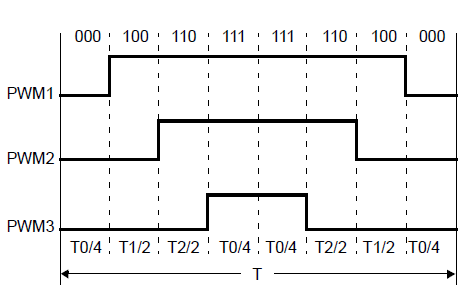
我们看一下空间全矢量的合成动图：

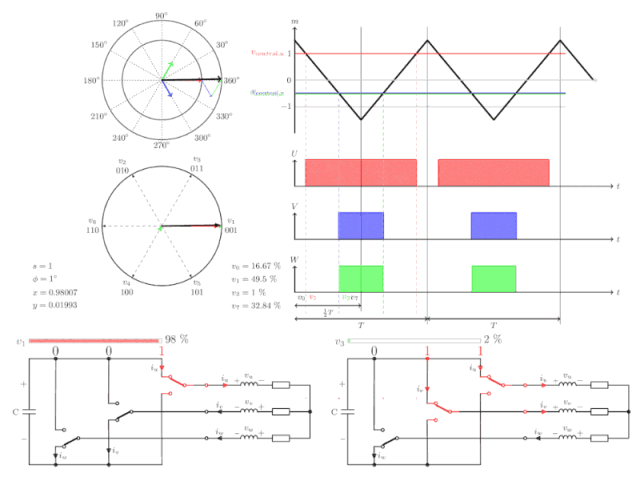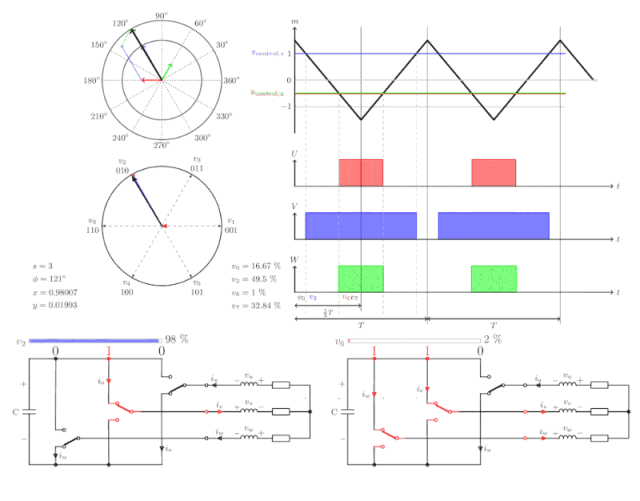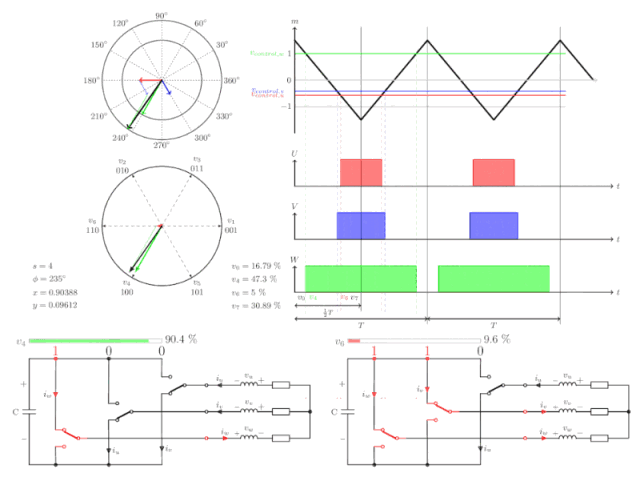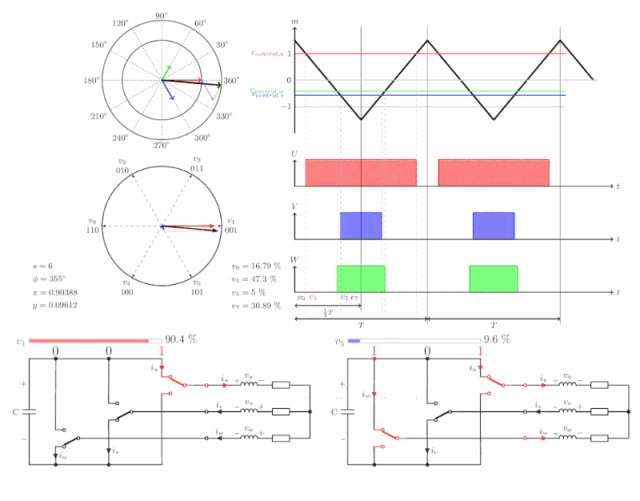
关于FOC矢量控制还有很多细节有待研究，本篇仅对FOC的基本原理做了简单说明，后续有机会再做一些较为深入的分析。

• 上一篇： 电脑主机前面耳机插孔无声音，realtek
• 下一篇： MFC多语言实现的坑